Matriks 3 (Determinan & invers)

Matriks 2 (Operasi Matriks)

 

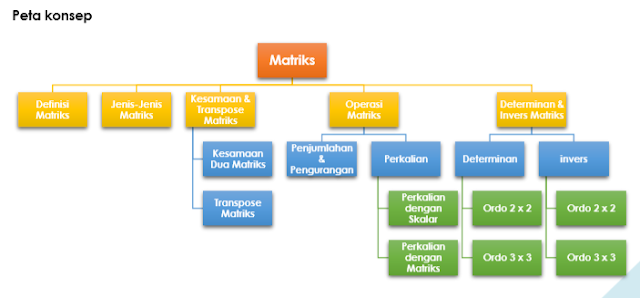
MATRIKS 1 (Definisi, Jenis-jenis, Kesamaan & Transpose Matriks)

A.   RINGKASAN MATERI

1.    Pengertian Matriks

a.    Definisi Matriks

Matriks merupakan susunan bilangan berbentuk persegi atau persegi panjang yang diatur dalam baris dan kolom serta dibatasi dengan tanda kurung. Bilangan-bilangan penyusun matriks disebut dengan elemen matriks. Sedangkan ukuran yang menyatakan banyaknya elemen matriks dinamakan dengan ordo matriks. Matriks dinotasikan dengan huruf kapital A, B, C, dan sebagainya.

Matriks A diatas berordo mxn, atau dinotasikan dengan A_mxn.

Contoh :

Hasil pertandingan sepak bola antara SMK Garuda dan SMK Tunas Bangsa tercatat dalam table berikut :

SMK	SKOR
	BABAK 1	BABAK 2
GARUDA	5	1
TUNAS BANGSA	3	4

Data tersebut dapat disederhanakan dengan menghilangkan semua keterangan (judul baris dan kolom) pada table dan mengganti table dengan tanda kurung, seperti berikut :

, baris 1 dan baris 2 menyatakan perolehan skor masing-masing sekolah, sedangkan kolom 1 dan 2 menyatakan peolehan skor tiap babak.

Jika matriks  kita sebut dengan matriks A, maka :

ü  5 merupakan elemen dari baris ke-1 kolom ke-1, atau a₁₁

ü  3  4  merupakan elemen baris ke-2

ü merupakan elemen kolom ke-1

b.    Macam-macam Matriks

1)      Matriks baris, merupakan matriks yang hanya terdiri atas satu baris.

2)      Matriks kolom, merupakan matriks yang terdiri dari satu kolom.

 

3)      Matriks nol, matriks yang elemen-elemennya nol.

 , merupakan matriks identitas untuk penjumlahan.

4)      Matriks identitas, matriks persegi yang elemen diagonal utamanya adalah 1 dan elemen lainnya nol.

 

5)      Matriks diagonal, matriks persegi dengan pola semua elemennya bernilai nol, kecuali elemen diagonal utamanya yang tidak semuanya bernilai nol.

 

6)      Matriks scalar, matriks yang elemen diagonal utamanya adalah bilangan yang sama selain nol, sedangkan elemen lainnya nol.

 

7)      Matriks persegi, matriks dengan banyak baris dan kolomnya sama.

 

8)      Matriks simetri, matriks persegi yang elemen pada baris ke-I dan kolom ke-j sama dengan elemen pada baris ke-j kolom ke-i.

 

9)      Matriks segitiga, matriks persegi yang elemen-elemen dibawah atau diatas diagonal utama semuanya adalah nol.

c.    Kesamaan Matriks

Dua buah matriks dikatakan sama jika ordo kedua matriks sama dan  elemen-elemen yang seletak (bersesuaian) nilainya sama.

Contoh :

d.    Transpose Matriks

Perubahan posisi elemen matriks pada baris menjadi kolom dan kolom menjadi baris dinamakan dengan transpose matriks. Transpose matriks dinotasikan dengan A^T.